Following this thermistor tutorial i used 1k thermistors (and resistors) instead of 100k as in video.
Skip to the end to get the easy answer!
Your choice of thermistor and bias resistor values depends on the following: 1. How much current do you want to spend? 2. How do you want the thermistor resistance to compare with the wiring resistance? 3. How much filtering do you need? 4. What kind of linearization do you want to apply?
A lower value thermistor will pull more current than a higher value one. More current means less battery life but also affects (2) and (3) below.
For a given system wiring resistance, increasing the thermistor resistance reduces the measurement error due to the wiring. If your thermistor is 100 ohms (25C nominal) and your wiring is 1 ohm, then you would have a 1% error at 25C. For an NTC (Negative Temperature Coefficient) thermistor, as it gets hotter and it resistance decreases, the wiring error increases because the wiring represents a greater percentage of the total resistance.
Filtering a resistive sensor in front of an ADC can be done by simply putting a capacitor across the ADC input. As your sensor resistance increases, the size of the capacitor required decreases for the same cutoff frequency. Even if filtering is not needed, be sure to check the ADC input impedance requirement as sample and hold circuits need their minimum AC input impedances to be satisfied as well as the DC input currents: Too much sensor impedance does not go well with too high ADC input current.
Unless you are using a platinum RTD with its linear response curve, your thermistor resistance vs temperature curve is going to be logarithmic where each end of the curve will be asymptotic. This means you will get good resolution around the 25C reference temperature but at one end you'll get very little resistance change for a large change in temperature and at the other end you'll get a lot of resistance change for very little change in temperature. By putting a resistor in parallel with the thermistor you can flatten out the curve to fit your measurement needs.
All this being said, your best bet is to put the thermistor curve into a spreadsheet and adjust the values until you get current consumption you can live with with a curve that gives you the information you need. See this example for a 10K NTC sensor with linearization (Either the RT/R25 or RT-vs-Temp values are almost always listed in the data sheet for each thermistor): Spreadsheet for this graph
The standard way to measure a resistive sensor is to make a voltage divider with the sensor and a fixed resistance between Vcc and GND, like this:
Vcc
│
Rb
│
├─── analog input
│
Rx
│
GND
where Rx is the resistance you want to measure and Rb is a known bias resistance. The only unknown is the choice of the bias resistance.
The simple rule of thumb is to choose a bias resistance close to the typical values of the resistance you want to measure, as this will optimize your measurement resolution. More specifically, the relative measurement resolution, which could be stated as the number of ADC steps you get per percent change in resistance, is maximal when Rx = Rb, and decreases only slowly as Rx gets further from Rb.
Now, one could argue that the relative resistance resolution is not always the best performance metric. You may want to maximize the absolute resistance resolution instead, or maybe the absolute conductance resolution. Each of these choices would lead to a different choice of bias resistor. For the case of a thermistor, however, the choice is pretty clear: the resistance varies almost exponentially with temperature, which means that the absolute temperature variations are practically proportional to the relative resistance variations. If you want to use temperature resolution as a metric, you could go through a tedious calculation only to find out that the optimal Rb is darn close to Rx.
In short, if your thermistor is 1 kΩ at 25 °C, and you will use it near 25 °C, then a 1 kΩ pullup will give you the best temperature resolution.
Now, measurement resolution may not be the only issue you care about, and you may want to sacrifice some of it in order to improve something else. For example:
Current consumption: a 1 kΩ thermistor in series with a 1 kΩ pullup will draw 2.5 mA (assuming Vcc = 5 V), which could rise to near 5 mA if it gets really hot. If you are running off battery power this could be an issue.
Self heating: in that 1 kΩ + 1 kΩ configuration, the thermistor will dissipate 6.25 mW. I've seen the datasheet of a typical thermistor stating a thermal dissipation constant of 7 mW/K. This means the measurement current would heat the thermistor to 0.9 °C above ambient temperature, which you would need to take into account in your temperature calculations.
Both of these issues would be mitigated by using a larger value for Rb, only at the cost of measurement resolution. Switching to a 10 kΩ thermistor would mitigate these issues without sacrificing resolution.
Related:
I was trying to figure this out myself and was going to ask a question to verify my results. Since this question is so close, I'll just post my results as an answer and comments/votes can help me figure out if it's correct!
I've been going by this tutorial on Adafruit which, unfortunately, doesn't talk about why they use a 10k Ohm thermistor paired with a matching fixed/bias resistor.
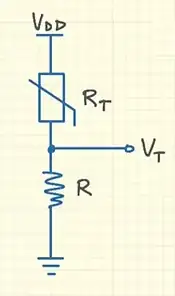
So we're on the same page, here's the circuit used (voltage divider, pic taken from the second related answer above):
The formula used to get from resistance to temperature (taken from the Adafruit guide, which uses the Steinhart-Hart equation):
Here's the full code used to find the temperature based on the voltage divider created by the fixed/bias resistor and the thermistor:
int pin_therm = A0; // analog read pin
float reading; // hold thermistor resistance
float stein; // hold calculated temp
int res_fixed = 10000; // 10k fixed resistor
int res_therm = 10000; // 10k thermistor
int therm_nom = 25; // nominal thermistor temp
int therm_b = 3950; // thermistor B coefficient
reading = analogRead(pin_therm);
reading = (1023 / reading) - 1;
reading = res_fixed / reading;
// apply the S-H equation
stein = reading / res_therm; // (R/Ro)
stein = log(stein); // ln(R/Ro)
stein /= therm_b; // 1/B * ln(R/Ro)
stein += 1.0 / (25.0 + 273.15); // + (1/To)
stein = 1.0 / stein; // Invert
stein -= 273.15; // convert to C
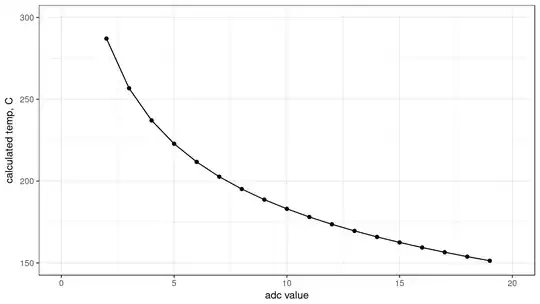
My aim is to measure around 150-250C, and I was curious what my resolution was after seeing very specific, "steppy" values when watching serial output. For example, as temps rose I'd see values like 202, 211, 222 but nothing in between.
I used R to send all possible ADC values of 0-1023 through the equation to find the corresponding calculated temperature.
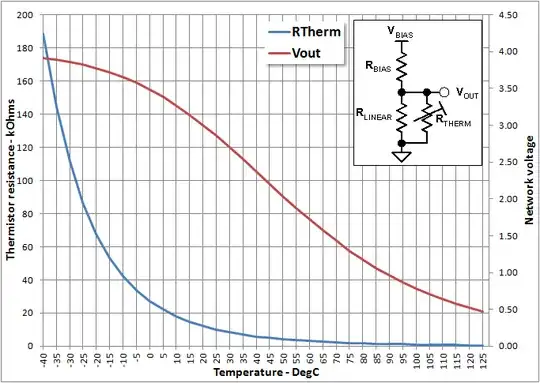
In my case, I modified the code above for the Honeywell 135-104LAG-J01 thermistor I was using (T = 25C, B = 3974). Using the rule of thumb to match the fixed resistor, here's what I get with 100k Ohms, showing ADC values for 150-250C. It revealed that this setup would only give me ~5 readings over 200-250C!
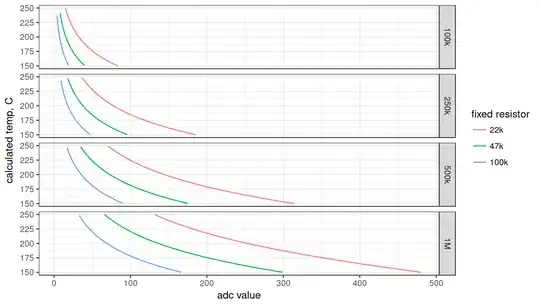
Going back to the math, it looked like I could drop the fixed resistance for better resolution. Here is the same 100k thermistor, but comparing the resolution obtained with 22k, 47k and 100k fixed resistors:
Using a lower fixed resistor, I have substantially more data points in my range of interest! We can simply compare the ADC ranges that make up this 150-250C span: ~20 for 100k and ~80 for 22k.
I'm not really worried about current consumption, but since it came up in the other answers, we can also increase the thermistor nominal resistance. Here's a plot breaking down by thermistor (100k - 1M) and matching fixed resistor (same 22k-100k values). I've removed the dots to make it less busy and the gray "mini-plot" titles are the thermistor values I looked at:
Lastly, to spare you from having to calculate the min vs. max ADC ranges covering the desired 150-250C range, here's a simple bar plot showing how many steps we get in this range.
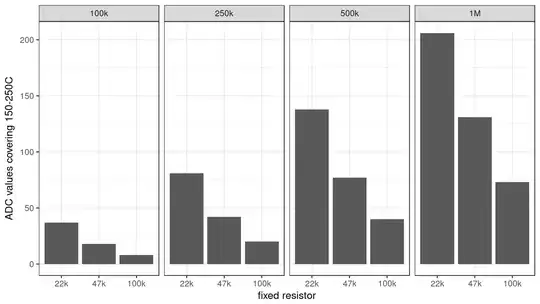
So, with a 1M Ohm thermistor and 22k fixed resistor, we could have ~0.5C resolution in this high range (100C span divided by ~200 ADC steps).
I echo the suggestion of John Taylor to plot things out, but in my case, the datasheet didn't list the key values required for his spreadsheet. I think spelling out the Adafruit code and putting my R code at the end can help understand how to do this (approximated) in order to compare temperatures of interest vs. ADC steps which cover it.
As a last aside, I ran into the mention of "source impedance" on one of the related questions. I'm not an electrical engineer, but some answers suggest that there may be a time delay issue with reading ADC values when the circuit resistance is very high:
That said, since I'm measuring high on the temp scale, an NTC thermistor will have less than max resistance. We're also helped by the fact that the equivalent resistance is:
1/((1/R_fixed) + (1/R_therm))
So, even with a 1M thermistor an 100k fixed, our equivalent resistance at room temperature is:
1/((1/1000000) + (1/100000)) = ~91k
This will only reduce further at higher temps, but I thought I'd mention it for the sake of thoroughness!
Here's the R code used to generate the multi plot covering 100k-1M thermistors vs. 22k-100k fixed resistors:
## for plotting
library(ggplot2)
## R kept wanting scientific notation, e.g. 10e5
options(scipen=10)
## range for ADC reading
inputs <- 0:1023
## create all combos of fixed resistor, thermistor, and ADC values
combos <- expand.grid(res = c(22000, 47000, 100000),
therm = c(100000, 250000, 500000, 1000000),
adc = 0:1023)
## make sure it's sorted the right way
## also, give it a unique identifier per combo
combos <- combos[order(combos$therm, combos$res, combos$adc), ]
combos$grp <- paste0(combos$res, "_", combos$therm)
## calculate the temps for each thermistor/fixed res combo
dat_lst <- lapply(unique(combos$grp), function(grp) {
temp <- combos[combos$grp == grp, ]
res <- unique(temp$res) / ((1023 / inputs) - 1)
stein <- res / unique(temp$therm);
stein <- log(stein);
stein <- stein / 3974.0;
stein <- stein + (1.0 / (25.0 + 273.15));
stein <- 1.0 / stein;
stein <- stein - 273.15;
temp$temp <- stein
return(temp)
})
## combine results
data <- do.call(rbind, dat_lst)
## some factor re-labeling to make plots more readable
data$res <- factor(data$res,
levels = c(22000, 47000, 100000),
labels = c("22k", "47k", "100k"))
data$therm <- factor(data$therm,
levels = c(100000, 250000, 500000, 1000000),
labels = c("100k", "250k", "500k", "1M"))
## reduce to only values in our range of interest
data <- data[data$temp > 150 & data$temp < 250, ]
## the plot itself
p <- ggplot(data, aes(x = adc, y = temp, colour = as.factor(res),
group = grp)) + geom_line()
p <- p + scale_x_continuous("adc value")
p <- p + scale_y_continuous("calculated temp, C")
p <- p + facet_grid(therm ~ .) + theme_bw()
p <- p + scale_colour_discrete("fixed resistor")
p
## to save it out
png("./therm-vs-fixed.png", res = 200, width = 1600, height = 900)
p
dev.off()
