How to emulate an analog potentiometer with PWM

Question

I have a piece of electronic that controls a motor. It takes power from AC power.

Now there is a 10KOhm Potentiometer. The data sheet of this controller says that the control signal is 10Vcc.

Here's the connections diagram (in Italian):

I'd like to emulate the Potentiometer with Arduino. I'm not sure if PWM will do the job.

Any hints?

Answer 1

You can take an analog (PWM) output from the Arduino and turn it into 0 to 10 V DC using something like this:

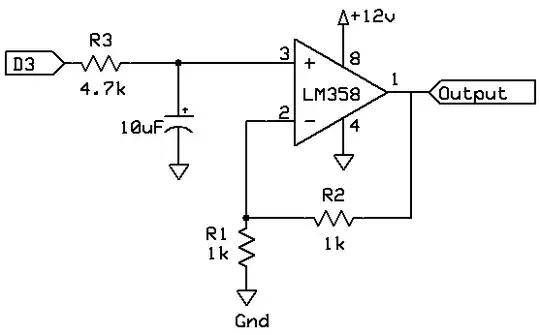
Amplification

The op-amp shown is hooked up as a non-inverting amplifier, where the gain is given by:

V_Out / V_In = 1 + (R2 / R1)

Since R2 and R1 in this case are both 1 k then the output will be the input multiplied by:

1 + (1000/1000) = 2

Thus, if we have 5 V coming from D3 we will have 10 V at the output of the op-amp. We need to supply a bit more than 10 V to the op-amp supply pin (pin 8) because this is not a rail-to-rail op-amp, that is, it cannot output all the way up to its supply voltage.

---

Low-pass filter

The resistor R3 and the 10 µF capacitor form a low-pass filter that filters the PWM signal from the Arduino into a more-or-less smooth DC voltage.

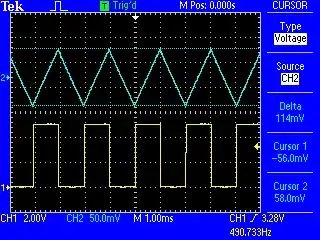
This shows the difference between the Arduino PWM output, and the output of the op-amp:

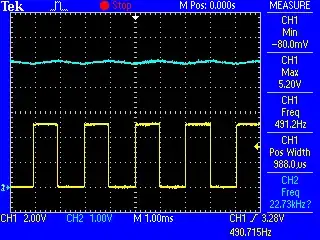
You can see from the scope traces that the yellow line (the PWM output) has a 50% duty cycle, and the blue line (the op-amp output) is 5 V and has a slight ripple.

With a 100% duty cycle, the output is 10 V.

---

Ripple

Switching the scope to AC coupling we can see how much ripple we have in the op-amp output:

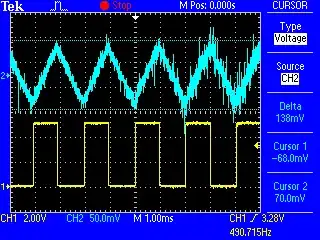
The scale for the blue channel has changed in this image, and the cursor shows that we have around 140 mV of ripple.

We can reduce the ripple by using a larger resistor for R3. For example, making it 10 k reduces the ripple to 86 mV.

The larger resistance make the output less responsive to changes at the input (it takes time to charge or discharge the capacitor) but in testing it still seems pretty responsive.

---

Code

Test code:

void setup () 
  { 
  }

void loop () 
  {
  analogWrite (3, analogRead (A0) / 4);
  }

I had a potentiometer connected to A0 and adjusted it to alter the duty cycle of the PWM output on pin D3.

---

Theory

You might ask "Why 138 mV of ripple? Why not 50 mV? Why not 200 mV?".

Let's look at the theory. First, the image posted above looks a bit noisy, so let's take an average of the input to the op-amp:

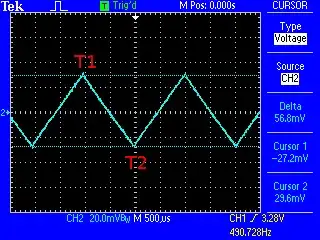
Now we can see that the ripple is about 57 mV (the output of the op-amp would be double that). Indeed, the averaged output is 57 * 2 = 114 mV

The general formula for calculating the time taken by a RC network to reach a certain voltage is:

t = -log((V-Vc)/V)R*C

Where "exp" is the natural exponent.

See Ladyada - RC Delay Calculator.

Also Mathematical treatment of charging and discharging a capacitor.

V  = supply voltage   (initial voltage)
Vc = output voltage   (target voltage)
R  = resistance in ohms
C  = capacitance in farads
t  = time in seconds

These figures will be on the RC discharge graph at roughly the point indicated:

See Wikipedia - RC circuit

Introducing our values for the resistor and capacitor (using Lua) we get:

VS = 5.0       -- supply voltage
VMED = VS / 2  -- 50% duty cycle
VL = VMED - 27.2e-3   -- low voltage as measured
VH = VMED + 29.6e-3   -- high voltage as measured
RES = 4700            -- resistance in ohms
CAP = 10e-6           -- capacitance in farads

T1 = -math.log ( (VS - VH) /VS) * RES * CAP 
T2 = -math.log ( (VS - VL) /VS) * RES * CAP 

print ("T1 =", T1)
print ("T2 =", T2)
print ("diff = ", T1 - T2, "seconds")

Results:

T1 = 0.0331
T2 = 0.0321
diff =  0.0010 seconds

The time difference is 1 ms which agrees with the observations.

Answer 2

Adding to Ricardo's answer:

PWM can do the job, sort of. You need a low pass filter (LPF) to convert the PWM to an analog voltage and an amplifier to take it from 0-5 to 0-10V. Or you can get a dedicated digital-to-analog (DAC) chip but that will obviously be more expensive than a resistor and capacitor for the LPF.

Here's some tutorials on converting your PWM to an analog voltage:

Analog-Output: How-To Arduino’s AnalogWrite – Converting PWM to a Voltage

Then you need to basically double the voltage. You do that with an operational amplifier. The resistors you pick for the op amp set its "gain", in this case you want it to be 2 so you can go from ~5v (max output) to 10v.

Here's an example of that: My First OP-AMP Circuit

Answer 3

You can use any typical motor control chip like a ULN2003 with PWM and maybe a smoothing capacitor, Google "ULN2003 Arduino" for many examples.

Based on the pinouts from Ricardo's answer, you'd get the 10V from pin 1 and ground from pin 3, and feed the PWM'd output from the ULN2003 back into pin 2.

Answer 4

I won't be able to answer your question completely, but hopefully I'll be able to make things a bit clearer for someone more knowledgeable to complete the answer.

From what I could understand from the datasheet, inputs 1, 2 and 3 are used to connect a pot that will control the motor speed. It's the POTENZIOMETRO DI COMANDO (control pot) in the figure linked in the question.

The datasheet also specifies (in the figure below) that you can connect terminal 3 to ground and feed terminal 2 with a voltage from 0 to 10Vcc, that will control the motor. That's how you control the motor using a MCU, I suppose.

Here's where my knowledge is getting short. I'm guessing that a PWM signal won't do the trick. You'll need to feed an actual voltage in terminal 2 to control the motor properly. To do that you have a few alternatives:

1. Use an ADC IC
2. Use an R2R resistor ladder network using digital outputs and some means to amplify its voltage to 10Vcc.

I hope this helps a bit.

Answer 5

my solution is simple get a servo (pwm input) and connect the shaft of the servo to the pot with a coupler then just use a simple servo control program